BISAC NAT010000 Ecology
BISAC NAT045050 Ecosystems & Habitats / Coastal Regions & Shorelines
BISAC NAT025000 Ecosystems & Habitats / Oceans & Seas
BISAC NAT045030 Ecosystems & Habitats / Polar Regions
BISAC SCI081000 Earth Sciences / Hydrology
BISAC SCI092000 Global Warming & Climate Change
BISAC SCI020000 Life Sciences / Ecology
BISAC SCI039000 Life Sciences / Marine Biology
BISAC SOC053000 Regional Studies
BISAC TEC060000 Marine & Naval
On the base of laboratory experiment a nonlinear wave transformation above underwater reef and trench was investigated. It was revealed that underwater trench and reef can decrease the mean wave period. Dependencies of changes of mean wave period and significant wave height on relative length of underwater structure and water depth above it were obtained. The changes of symmetry of waves passing above underwater structures are discussed.
underwater structures mean wave period, symmetry of waves.
I. Introduction
The storm waves are the main source of energy in a coastal zone. Their impact on the coast is significant and a protection of the shore against the waves is an important problem of coastal engineering. Often for this purpose different underwater structures are used, for example, artificial submerged reefs or trench.
Artificial reef can have various configurations. It can be of spherical, cone-shaped, semi-spherical form or a block from a metal wire grid filled of stones. The reef can be also simple created by concrete elements of special design chaotically placed on bottom relief.
The main difference of reefs from other submerged structures is a permeability that provides minor influence on water exchange and water quality in the coastal area. Underwater trench is also very simple constructed structure having many advantages, especially concerning a transport of deposits due to wave’s action in coastal zone. The trench and reef are ecological-friendly as for seas habitants and for recreation purposes in coastal zone management. Usually wave breaking and decreasing of wave energy are main features taking in account when wave transforming above submerged structure. Than less is the water depth above the top of submerged structure than more intensive will be wave breaking and reducing of wave energy. Another effect of wave transformation above submerged structure is nonlinear wave decomposition and formation of secondary waves consisting from highest nonlinear wave harmonics that decreases the effect of wave impact on the shore too.
The basic nonlinear-dispersive mechanism of formation of secondary waves is described in details by many researchers [1, 2, 3, 4, 5]. Secondary waves arise as separate peaks on a surface of initial wave and consist from higher harmonics of main wave motion. Higher harmonics are formed due to nonlinearity during the wave propagation above top of reef or on seaward part of trench on shallow water. Secondary waves are well visible behind the reef and in trench on relatively deeper water.
A decomposition of initial waves and formation of secondary waves leads to decreasing of mean wave period. It has many advantages for coastal engineering: 1) it can suppress or at least detain wave breaking and, accordingly, energy dissipation to a coastal line; 2) the shorter waves less affect on the bottom relief and on a coastal constructions; 3) decreasing of wave period permit to use the floating breakwaters for additional attenuation of wave motion [6]. So possibility to decrease the mean wave period may be very useful for innovation methods of shore protection and can be considered as additional feature of underwater structures as breakwaters.
The main aim of this work is experimental investigation of nonlinear transformation of waves above a single underwater reef and trench and parameterization of changes of wave parameters on dependence of parameters of underwater structure and initial parameters of waves.
II. Laboratory experiment
The physical experiments of transformation of waves above underwater structures were carried out in the flume of Scientific Center “Sea shores” in Sochi, Russia, in 2013. The length of flume is 22 m, width – 0.6 m, height – 1 m. One permeable reef and underwater trench were tested. Physical modeling was done in scale 1:20. A transformation of initially pseudo monochromatic waves was investigated.
Permeable reef was constructed from tetrapodes. The mean length of reef was about 0.4 m and the mean height – about 0.14 m. The reef was placed on inclined bottom with slope 0.022 (Fig.1). The underwater trench with mean length 1 m and mean depth 0.22 m was also constructed on inclined bottom (0.022) before a shore line. The bottom slope after trench up to shore line was 0.04 (Fig.2). Water depth for experiments was 0.4 m. In total 40 series of measurements were done for wave with periods from 1.4 up to 4 s and with initial heights from 0.2 up to 0.05 m. For the measurements of wave transformation 14 capacity wave gauges were used. Duration of wave records was 2-3 min with sampling frequency 50 Hz.

bottom friction: the trench is longer, the more is a loss of energy on friction. However height can become big because of effect of "shoaling" at an exit of waves from a trench on shallow water due to sharp reduction of water depth again.
.jpg)
The mean period determined by the spectral moments (4), practically in all analyzed series of data significantly doesn't change after passing of a trench. It can slightly decrease in a trench on seaward edge, at once at an exit of waves to deeper water (fig. 8), at distances less than 0.05 of relative length of trench (Fig. 8, the green line).
.jpg)
On deep water in a trench the amplitude of the highest harmonics don't increase because of weakening of nonlinear interactions therefore their small growth connected with reduction of depth at an exit from a trench at its coastal edge practically doesn't influence on change the mean period determined by the spectral moments (4). Increasing of the mean period in a trench and after it is connected with reflection of waves from the coast and from edges of a trench.
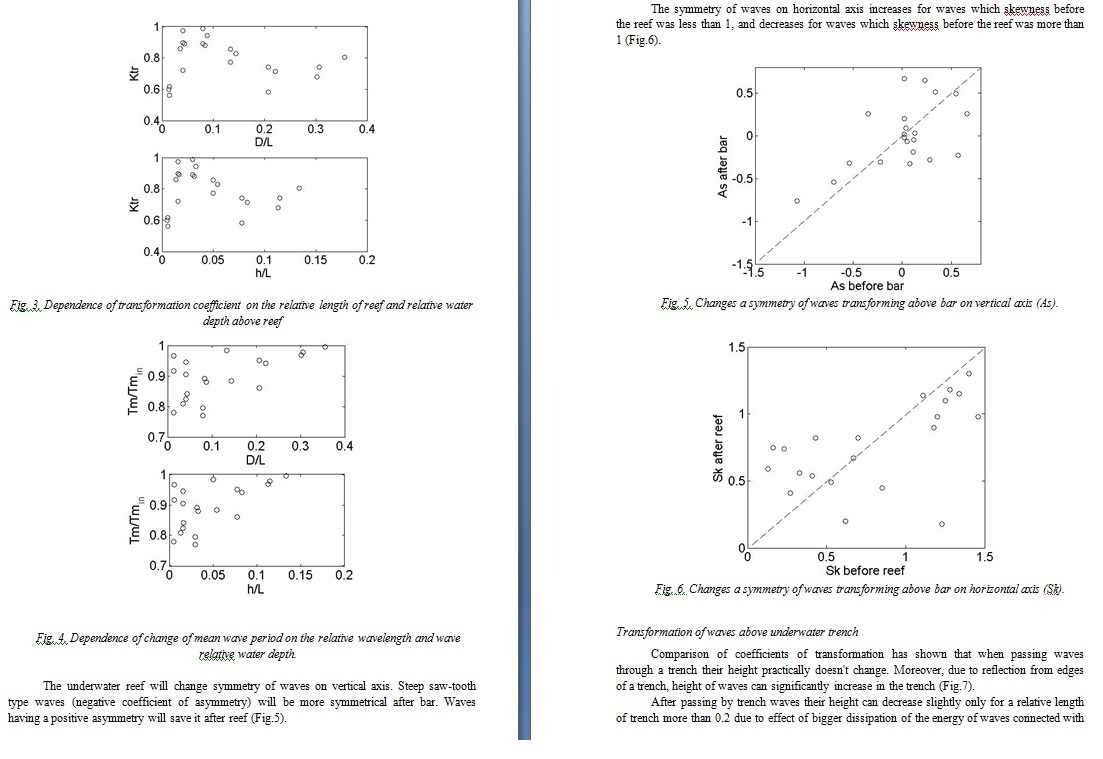
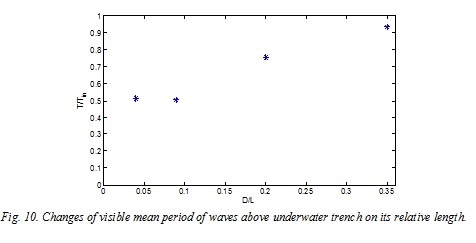
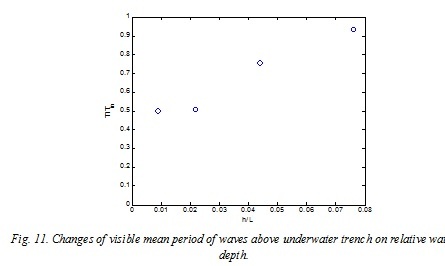
However the mean period determined by crossing of the average line can change significantly (twice) in a trench, and these changes will remain also at the exit from a trench (Fig. 9, 10, 11). On fig. 9, 10 and 11 the changes of the visible mean period of waves after passing of a trench on its relative length (D/L), on its relative depth of installation (h/L) and relative height of a wave are shown in seaward edge of a trench (Hs/h, where Hs – significant wave height, h – water depth), respectively.
The trench is longer, the less there will be changes of the period. The trench is longer, the waves of the highest harmonics are shifted behind more. They "catch up" with the next wave with the period of the main harmonic and the mean period becomes more again.
The shallower is a depth of installation of the trenches, the period can decrease more. As at smaller depth the amplitude of the highest harmonics will be more, and the waves formed by the highest harmonics will be better visible.
For steeper waves on an entrance to a trench, the period can change more. However, waves of the small steepness on very shallow water can also show decomposition of a crest and reduction of the period.
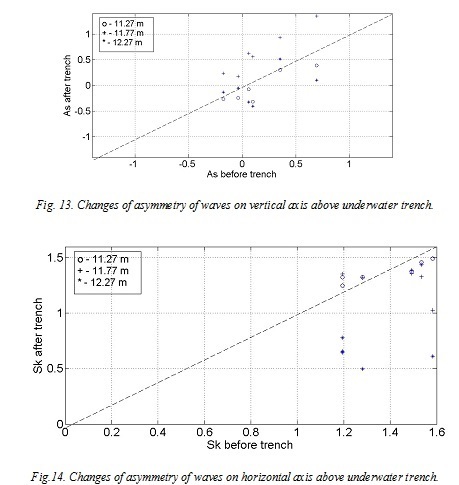
The trench changes vertical symmetry of waves to positive and reduces horizontal symmetry (Fig. 12, 13).
The waves which aren't breaking before a trench will have the greatest changes. The more the breaking of waves lasts, the their symmetry changes less. I.e. most effectively on change of asymmetry of waves the trench will "work" if to put it at a depth where waves only begin to break or at depth where the waves are close to height limit for the breaking waves.
IV. Conclusions
Physical modeling of waves passing above reef and trench has testified the possibility of essential decreasing not only wave height, but the mean period of waves also.
Dependences of transformation coefficient and changes of mean wave period on relative length (relation between a length of structure and wavelength on deep water) were obtained.
It was shown that underwater structure can change asymmetry of waves.
V. Acknowledgement
This work was supported by project 15-05-04649 of Russian Foundation for Basic Research
1. Beji, S., Battjes, J.A., “Experimental investigation of wave propagation over a bar”, Coast. Eng. 19, 1993,p.p.151-162.
2. Masselink, G., “Field investigation of wave propagation over a bar and the consequent generation of secondary waves”, Coast. Eng. 33, 1998, p.p.1-9.
3. Van der Meer, J.W., Regeling H.J., De Wall J.P. “Wave transformation: spectral changes and its effects on run-up and overtopping”. ASCE, Proc. 27th ICCE, Sydney, Australia, 2000.
4. Kuznetsov S. and SaprykinaY., “Mechanism of formation of secondary waves in coastal zone”, Proc. of Int. Conf. on Coastal Dynamics , 2009, Tokyo, Japan, World scientific.
5. Kuznetsov S. and SaprykinaY., “Secondary waves in coastal zone: physical mechanisms of formation and possible application for coastal protection”. Proceeding of 33th International Conference on Coastal Engineering, ed. by J.McKee Smith, World Scientific, 2012.
6. Kuznetsov S, Saprykina Ya., “Combinations of submerged structures and floating breakwater for shore protection”. Coastal Structures 2011. Proceedings of the 6th International Conference on Coastal Structures Yokohama, Japan, September 5-9, 2011, Ed. by Shigeo Takashi, Masahiko Isobe, Nobuhisa Kobayashi and Ken-ichiro Shimosako, World Scientific, p.p. 48 - 58.
7. SP32-103-97 “Design of coastal protection structures”, http://www.znaytovar.ru/gost/2/SP_3210397_Proektirovanie_mors.html.







